This series of posts was inspired by the notable exploits of Marcus Trescothick in 2009 (well, we Somerset supporters think they're notable, whether you do or not). He was the English season's leading scorer, amassing 2,934 runs across all competitions, and deserved winner of the PCA's 2009 MVP award as well as their Players' Player of the Year.
One particular milestone is that Trescothick's career batting average has, at the end of the current season, risen above 40, for the first time since he opened his first-class account (in a remarkable 1993 match that Somerset fans remember fondly for reasons that have nothing to do with the debutant). Admittedly, this doesn't sound like so momentous a watershed for a performer of supposed world class, especially in this run-heavy era. These days, after all, there are players who consistently average over 40 without causing much more than a faint blip on the international radar. However, to understand quite what an achievement it has been for Trescothick to drag his average above this level, it needs to be emphasised quite how poor – and quite how prolongedly poor – the first part of his career was.
When he made his test debut – v. West Indies in 2000 – Trescothick had a batting average of 30.60 from 168 first-class innings. (The identification of a true talent hiding beneath that less-than-mediocre record is one of the few shreds of evidence that Duncan Fletcher knows the first thing about cricket, if you ask me.) Trescothick, of course, made a confident 50 in his first test innings, and never looked back. For the next few years, his cricket was played almost exclusively for England (in 2004, he didn't play a single game for Somerset) and his successful international career provided a substantial fillip to his average. By the time he played his last first-class game in England colours (that infamous encounter with Pakistan at the Oval in 2006), his average had risen to 35.75 from 360 FC knocks.
Since the beginning of 2007 – for reasons that have been documented, where they have not been fabricated, elsewhere – Trescothick has been a Somerset cricketer exclusively. Undoubtedly, England have been the poorer for his absence; you'll forgive us Taunton regulars a little parochialism if we don't entirely share the regret felt by cricket fans in other corners of the country. Across those three seasons, he has scored 4,418 runs in 48 FC matches at an average of 60.52.
2009 has been Trescothick's best season yet. He has scored 1,817 FC runs at 75.70, with 8 centuries. Only Jimmy Cook (11 in 1991 & 9 in 1990), Bill Alley (10 in 1961), and Viv Richards (9 in 1985) have scored more tons in a season for Somerset, and each of them had more matches in which to do so. In the process, he has passed 10,000 FC runs for the county. And when he was dismissed for 102 in the match against Lancashire at Taunton earlier this month, his average – at long last, 436 innings into his FC career – rose above 40.
So what may be remarkable about Trescothick's career trajectory is how he has slowly-but-steadily dragged himself up by the pad-straps from a distinctly unpromising beginning to arrive at a record that begins to do justice to his recognised abilities. Over on (everyone's favourite Somerset CCC messageboard) www.grockles.com, Loyal of Lhasa commented:
MT has now played for almost seventeen seasons and it is in this season that he has scored 10% of his career aggregate. I'm not sure how significant that is...
This struck me as a rather interesting question, so I did a bit of research on it, which led on to a bunch of additional questions.
There are two important notes to make about the analyses that follow. Firstly, they all revolve around calendar years rather than seasons. This is partially for the bad reason that it's much easier to extract years from my database, but also for the good reason that it makes observations slightly less noisy (lessening the possibility that a few freak innings might dominate the period in question). Secondly, all these analyses look at run aggregates alone when, in several instances, we might more naturally think in terms of batting averages. After all, no two years provide exactly the same opportunity to score runs, which is where the average comes in handy. My reliance on year-end aggregates isn't because I believe them to be some sort of superior metric for measuring a batsman's quality; it's just because they're what I'm interested in at the moment, in the light of Trescothick's high-scoring year. Most of the analyses could be rerun using averages, etc.; if anyone's interested to see them, let me know.
A very good year
It turns out that the fact that Trescothick scored 10% of his career runs in a single season may not be very significant at all. More than half of the 838 batsmen with 10,000 FC runs or more have gone through a calendar year in which they scored a higher proportion of their career runs than Trescothick has this year. Top of the lot is David Hussey, who racked up over a quarter of his life's runs in 2007. Below are the top few and the bottom few and a few notable anni mirabiles ('scuse slight Somerset bias) from in-between:
Table 1: The proportion of a batsman's career runs scored in his highest-scoring calendar year
Name CareerYrs CareerRuns BestYr BestYrRuns % 1. DJ Hussey 7 10,048 2007 2,722 27.1% 2. AR Morris 14 12,614 1948 3,149 25.0% 3. FMM Worrell 22 15,025 1950 3,738 24.9% 4. VM Merchant 21 13,470 1946 3,224 23.9% 5. J Darling 14 10,635 1899 2,530 23.8% 6. CF Walters 13 12,145 1933 2,832 23.3% 7. PA Jaques 9 11,707 2005 2,728 23.3% 8. ED Weekes 19 12,010 1950 2,749 22.9% 9. BC Booth 14 11,265 1964 2,536 22.5% 10. RM Cowper 11 10,595 1964 2,344 22.1% 11. CJL Rogers 12 12,464 2006 2,705 21.7% 12. J Ryder 21 10,501 1921 2,247 21.4% 13. JC Adams 18 11,234 1994 2,375 21.1% 14. WJ Cronje 13 12,103 1995 2,551 21.1% 15. CG Macartney 21 15,019 1921 3,147 21.0% 16. CH Gayle 12 11,256 2001 2,325 20.7% 17. MD Crowe 16 19,608 1987 4,045 20.6% 18. GHG Doggart 14 10,054 1949 2,063 20.5% 19. KR Stackpole 14 10,100 1972 2,053 20.3% 20. WA Brown 16 13,838 1938 2,793 20.2% ... 31. VT Trumper 19 16,939 1902 3,220 19.0% ... 56. BC Lara 20 22,156 1994 3,828 17.3% ... 68. WH Ponsford 14 13,819 1930 2,311 16.7% ... 84. RN Harvey 18 21,699 1953 3,506 16.2% ... 108. DG Bradman 20 28,067 1930 4,368 15.6% ... 118. SJ Cook 24 21,143 1991 3,234 15.3% ... 172. MEK Hussey 16 19,242 2001 2,711 14.1% ... 265. DCS Compton 22 38,942 1947 4,962 12.7% ... 456. ME Trescothick 17 16,645 2009 1,817 10.9% ... 522. L Hutton 19 40,140 1948 4,167 10.4% ... 595. GS Sobers 22 28,314 1968 2,745 9.7% ... 701. WR Hammond 26 50,551 1933 4,422 8.7% ... 714. H Sutcliffe 22 50,670 1932 4,373 8.6% ... 716. GA Hick 26 41,112 1988 3,540 8.6% 717. SR Waugh 21 24,052 1988 2,071 8.6% ... 725. IVA Richards 22 36,212 1976 3,080 8.5% ... 827. G Boycott 25 48,426 1970 3,109 6.4% 828. PA Perrin 29 29,709 1906 1,893 6.4% 829. EM Grace 33 10,025 1883 638 6.4% 830. CT Radley 24 26,441 1975 1,667 6.3% 831. A Jones 27 36,049 1963 2,159 6.0% 832. KWR Fletcher 27 37,665 1968 2,248 6.0% 833. G Gunn 27 35,208 1908 2,032 5.8% 834. FE Woolley 29 58,959 1929 3,389 5.7% 835. WG Quaife 31 36,012 1905 2,060 5.7% 836. JB Hobbs 26 61,760 1914 3,524 5.7% 837. DB Close 35 34,994 1959 1,990 5.7% 838. WG Grace 44 54,211 1871 2,739 5.1% figures correct at end of English FC season 2009; full list available here
The problem with this mode of analysis is that it doesn't take account of the length of a batsman's career. As Loyal of Lhasa responded,
at the end of one's first season one has by definition scored 100% of one's career runs in a single season.
Accordingly, it is no surprise to see some of the longest FC careers at the bottom of the list (to have joined the 10% club, Grace, Hobbs, or Woolley would have had to amass more than 5,000 of their runs in a single year). Back on www.grockles.com, Frome Exile made some similar comments:
[David] Hussey has a quarter of his runs in one seventh of his "years" which is hardly as remarkable as [Arthur] Morris' quarter of his runs in one fourteenth of his years.
Perhaps a more interesting analysis, then, would be one that attempted to capture the extent to which a batsman's best season was truly exceptional, when compared with the rest of his career. Perhaps you could weight the percentage figure according to the number of seasons played; mathematically, this is identical to finding the batsman's mean year score (i.e. what you'd typically expect him to score in any given year), and calculating the ratio of the exceptional year to the typical one. For example, when WG Grace scored 2,739 runs at the height of his early-career rampage in 1871, that was over twice as much as the 1,232 runs he scored per year on average throughout his career; in contrast, Hobbs's 1914 aggregate was only 48% higher than the 2,375 runs you could expect from him in any given year. So, of course, Frome Exile is entirely right: David Hussey's 2007 runfest amounted to a total that was 90% higher than his typical year's tally, whereas Morris's 1948 aggregate was three-and-a-half times higher than he managed, on average, through his career.
There's a problem with taking a simple ratio of extreme:mean, though, and that's that what makes an extreme observation unusal is not just its relationship to the mean, but how it corresponds to the whole set of observations. Statisticians would say we are interested in how the variable is distributed. To illustrate the importance of this, consider the following: The mean weight of males aged 20 or over is 13st 12lb, so someone who is 20% above average would be 16st 9lb (i.e. a bit of a porker, but nothing outlandish: the kind of bloke you pass in the street every day without thinking anything of it). On the other hand, the mean height of males aged 20 or over is 5'9", but someone who is 20% above average would be 6'11" (i.e. really quite unusually monstrous: the kind of bloke you certainly do notice when you pass him in the street). So the same 20% increment can produce results that are more or less exceptional, depending on the way the observations are distributed.
Fortunately, there is a well established way to quantify the exceptional-ness of a particular observation within a distribution. That method is the z-score. To calculate a z-score, one needs to know the mean and the standard deviation of the distribution in question; the z-score is simply the number of standard deviations between the extreme observation and the mean.
(Note for stats-heads: I did a bit of analysis, and it turns out that calendar-year aggregates tend to be pretty normally distributed. Although there's no reason why z-scores can't be calculated for asymmetric – and other non-normal – distributions, it's reassuring to know that we're not dealing with anything kinky, here.)
Calculating the z-score for each batsman's most productive year gives the following list:
Table 2: Batsmen's highest-scoring calendar year, compared to the rest of their careers, in terms of z-score
Name CareerYrs CareerRuns Avg. ± SD BestYr BestYrRuns z 1. CK Nayudu 41 11,825 288 ± 346 1932 1,893 4.64 2. B Sutcliffe 25 17,447 698 ± 723 1949 3,493 3.87 3. FMM Worrell 22 15,025 683 ± 792 1950 3,738 3.86 4. Mansoor Akhtar 23 13,804 600 ± 494 1987 2,328 3.50 5. Saleem Malik 22 16,586 754 ± 555 1991 2,693 3.49 6. J Ryder 21 10,501 500 ± 514 1921 2,247 3.40 7. BC Lara 20 22,156 1108 ± 811 1994 3,828 3.35 8. MH Mankad 29 11,593 400 ± 300 1946 1,402 3.34 9. ED Weekes 19 12,010 632 ± 641 1950 2,749 3.30 10. RF Pienaar 21 10,896 519 ± 468 1989 2,061 3.29 11. KD Mackay 19 10,823 570 ± 459 1956 2,079 3.29 12. VM Merchant 21 13,470 641 ± 790 1946 3,224 3.27 13. DP Hughes 23 10,419 453 ± 270 1982 1,303 3.15 14. JC Adams 18 11,234 624 ± 569 1994 2,375 3.08 15. P Roy 22 11,868 539 ± 470 1959 1,979 3.06 16. RN Harvey 18 21,699 1206 ± 753 1953 3,506 3.06 17. A Shrewsbury 27 26,505 982 ± 505 1887 2,520 3.05 18. RG Pollock 28 20,940 748 ± 338 1965 1,757 2.98 19. AW Nourse 30 14,216 474 ± 538 1924 2,076 2.98 20. HW Taylor 23 13,105 570 ± 501 1924 2,042 2.94 ... 56. VT Trumper 19 16,939 892 ± 879 1902 3,220 2.65 ... 68. SJ Cook 24 21,143 881 ± 913 1991 3,234 2.58 ... 81. DCS Compton 22 38,942 1770 ± 1272 1947 4,962 2.51 82. AR Morris 14 12,614 901 ± 896 1948 3,149 2.51 ... 87. GA Hick 26 41,112 1581 ± 791 1988 3,540 2.48 88. DG Bradman 20 28,067 1403 ± 1202 1930 4,368 2.47 ... 125. IT Botham 20 19,399 970 ± 469 1982 2,056 2.32 ... 145. WG Grace 44 54,211 1232 ± 669 1871 2,739 2.25 ... 156. SM Gavaskar 22 25,834 1174 ± 771 1971 2,890 2.23 ... 171. H Sutcliffe 22 50,670 2303 ± 941 1932 4,373 2.20 ... 204. FE Woolley 29 58,959 2033 ± 638 1929 3,389 2.13 ... 239. GA Gooch 26 44,846 1725 ± 871 1990 3,523 2.07 ... 359. MEK Hussey 16 19,242 1203 ± 798 2001 2,711 1.89 ... 369. ME Trescothick 17 16,645 979 ± 447 2009 1,817 1.87 ... 402. WH Ponsford 14 13,819 987 ± 727 1930 2,311 1.82 ... 410. GS Sobers 22 28,314 1287 ± 804 1968 2,745 1.81 ... 462. G Boycott 25 48,426 1937 ± 674 1970 3,109 1.74 ... 479. IVA Richards 22 36,212 1646 ± 833 1976 3,080 1.72 ... 514. WR Hammond 26 50,551 1944 ± 1468 1933 4,422 1.69 ... 576. L Hutton 19 40,140 2113 ± 1275 1948 4,167 1.61 ... 581. DJ Hussey 7 10,048 1435 ± 803 2007 2,722 1.60 ... 609. KS Ranjitsinhji 15 24,692 1646 ± 1044 1899 3,284 1.57 ... 704. JB Hobbs 26 61,760 2375 ± 798 1914 3,524 1.44 ... 819. KP Pietersen 12 11,026 919 ± 564 2004 1,567 1.15 820. FC Holland 15 10,384 692 ± 381 1903 1,129 1.15 821. W Bates 11 10,249 932 ± 440 1885 1,433 1.14 822. E Cooper 10 13,304 1330 ± 515 1949 1,916 1.14 823. AJW Croom 18 17,692 983 ± 529 1931 1,584 1.14 824. HE Dollery 17 24,414 1436 ± 576 1949 2,084 1.13 825. KL Hutchings 11 10,054 914 ± 744 1908 1,744 1.12 826. B Lilley 15 10,496 700 ± 338 1928 1,074 1.11 827. RDB Croft 21 12,365 562 ± 216 1995 801 1.10 828. MS Nichols 16 17,823 1114 ± 501 1933 1,661 1.09 829. HW Stephenson 17 13,195 776 ± 336 1953 1,143 1.09 830. SA Marsh 18 10,098 561 ± 322 1990 911 1.09 831. R Kilner 13 14,707 1131 ± 420 1913 1,586 1.08 832. G Barker 18 22,286 1238 ± 468 1960 1,741 1.07 833. JT Brown 16 17,920 1120 ± 707 1896 1,873 1.07 834. D Brookes 21 30,874 1470 ± 720 1952 2,229 1.05 835. A Hamer 12 15,465 1289 ± 575 1959 1,850 0.98 836. LTA Bates 19 19,380 1020 ± 511 1926 1,518 0.97 837. C Lee 13 12,129 933 ± 601 1962 1,503 0.95 838. A Young 15 13,159 877 ± 390 1930 1,219 0.88 figures correct at end of English FC season 2009; full list available here
CK Nayudu's place at the top of this list is easily explained: for the majority of his career (a lengthy one: he played his last FC match aged 68!), Nayudu played a handful of games per year in India, amassing no more than a few hundred runs each time. Then, in 1932, he took part in India's inaugural test tour of the British Isles (during which he had the honour of captaining them in their first test match). That year, he played 55 FC innings, accumulating almost 2,000 runs. This single year is completely inconsistent with Nayudu's otherwise gentle career (it would be even more incongruous if he had not returned to England four years later, picking up just over 1,000 runs along the way).
Not far below Nayudu, we find Brian Lara's astonishing 1994 (the year during which, most memorably, he broke the records for both test and FC high-scores). Altogether, that year, he amassed almost 4,000 runs and, though the rest of his career was hardly a bust, that aggregate is more than twice as many as he managed in any other calendar year.
The player at the bottom of the list happens to be a Somerset player: "Tom" Young. Once he had established himself in the side of the 1920s, his season's aggregate was always very close to 1,000 runs so, when he recorded his personal best of 1,219 in 1930, it was the least exceptional best year of any collected here.
Figure 1: BC Lara and A Young – first-class runs per calendar year

So what about Trescothick? His 2009 is in the top half of the list, but there's nothing too remarkable about it. It is quite obvious that, impressive though it was, his best year does not share the sore-thumb status we saw in Lara's record.
Figure 2: ME Trescothick – first-class runs per calendar year
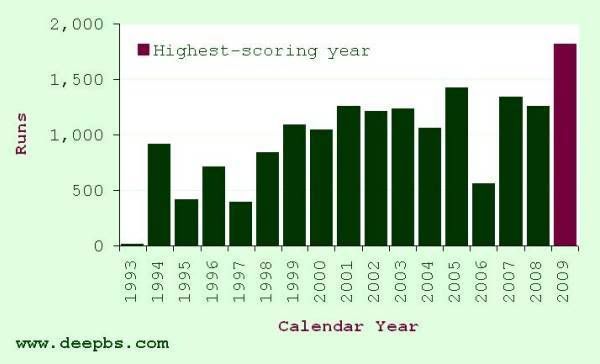
If we make one key assumption about batsmen's calendar-year aggregates (that they are normally distributed – which, by and large, they appear to be), we can quantify just how unexpected it was. A z-score of 1.87 corresponds to a probability of 0.969 (see here for an online calculator). In turn, this means that – in a career like Trescothick's, with a mean year's aggregate of 979 ± 447 – we would expect a batsman to score 1,817 runs or more one year in every [1/(1-p)=] 33 he played, as a result of simple random variation (i.e. even if his opportunities to accumulate runs – as well as his ability to score them – had remained constant over time). If Nayudu's career had followed a consistent course (without incongruous trips abroad), we would have expected one year like his 1932 every 575,753 years!
So Trescothick's 2009 falls into the category of good but not stand-out exceptional. To the extent that it fails to confirm our hypothesis about his apparently extraordinary year, this is a disappointing finding. On the other hand, it is arguably to Trescothick's credit: after all, it is only possible to set a conspicuous high-water mark if it stands in contrast to a typically lower level of achievement.
Indian summers
The next development came, once more, as a result of a comment from Loyal of Lhasa. He said,
I thought it interesting that Trescothick had probably taken rather a long time to get to [his best season], for he was hardly a speedy starter....
So I rejigged the stats, to see how far into each player's career his best calendar year came. The table below shows how many years each batsman had been playing for – BestYrNo – when he compiled the largest aggregate of his career (this is a count of years in which the player in question actually played FC cricket so, e.g., anyone whose career straddled a war does not have those years added to his total). As before, the dataset is limited to those amassing at least 10,000 FC runs.
Table 3: How late in his career each batsman's highest-scoring calendar year came
Name CareerYrs CareerRuns BestYr BestYrRuns BestYrNo 1. HTW Hardinge 28 33,519 1928 2,446 23 =2. EM Grace 33 10,025 1883 638 22 =2. JA Newman 24 15,364 1928 1,773 22 =4. R Abel 24 33,128 1901 3,309 21 =4. JH Board 25 15,674 1911 1,184 21 =4. GAR Lock 26 10,342 1966 831 21 =7. CP Mead 28 55,061 1928 3,745 20 =7. FE Woolley 29 58,959 1929 3,389 20 =7. CA Milton 27 32,150 1967 2,089 20 =7. JC Balderstone 24 19,034 1982 1,482 20 =7. SJ Cook 24 21,143 1991 3,234 20 =12. S Coe 24 17,438 1914 1,258 19 =12. AW Nourse 30 14,216 1924 2,076 19 =12. A Ducat 20 23,373 1930 2,067 19 =12. B Mitchell 22 11,395 1947 2,243 19 =12. DR Turner 24 19,005 1984 1,365 19 =12. AR Butcher 22 22,667 1990 2,116 19 =18. PF Warner 26 29,028 1911 2,274 18 =18. FA Pearson 23 18,734 1921 1,498 18 =18. JR Freeman 20 14,602 1926 1,958 18 =18. WRD Payton 23 22,132 1926 1,864 18 =18. AS Kennedy 26 16,586 1928 1,437 18 =18. Imtiaz Ahmed 24 10,393 1962 1,646 18 =18. EJ Barlow 25 18,212 1976 1,965 18 =18. JH Hampshire 24 28,059 1978 2,105 18 =18. P Willey 26 24,361 1983 2,036 18 =18. M Amarnath 24 13,747 1983 1,620 18 =18. GA Gooch 26 44,846 1990 3,523 18 =18. AJ Stewart 23 26,165 1998 1,986 18 =18. SC Ganguly 19 14,933 2007 1,391 18 =31. J Vine 23 25,171 1912 1,887 17 =31. EJ Smith 22 16,997 1925 1,477 17 =31. WE Astill 30 22,735 1926 2,218 17 =31. JWH Makepeace 21 25,799 1926 2,340 17 =31. EH Hendren 27 57,611 1928 4,024 17 =31. AE Dipper 21 28,075 1928 2,365 17 =31. CK Nayudu 41 11,825 1932 1,893 17 =31. VM Merchant 21 13,470 1946 3,224 17 =31. RWV Robins 25 13,884 1946 1,397 17 =31. GO Dawkes 18 11,411 1960 964 17 =31. B Constable 20 18,849 1961 1,799 17 =31. MH Denness 22 25,886 1975 1,904 17 =31. RW Taylor 27 12,065 1976 837 17 =31. JA Ormrod 24 23,206 1978 1,535 17 =31. BF Davison 21 27,453 1983 2,341 17 =31. P Carrick 22 10,300 1988 815 17 =31. NE Briers 22 18,726 1990 1,996 17 =31. HP Tillakaratne 22 13,258 2001 1,554 17 =31. S Chanderpaul 18 17,569 2008 1,709 17 =31. ME Trescothick 17 16,645 2009 1,817 17 ... =51. GS Sobers 22 28,314 1968 2,745 16 ... =109. H Sutcliffe 22 50,670 1932 4,373 14 ... =109. WR Hammond 26 50,551 1933 4,422 14 ... =272. DB Close 35 34,994 1959 1,990 11 ... =340. JB Hobbs 26 61,760 1914 3,524 10 ... =340. WH Ponsford 14 13,819 1930 2,311 10 ... =340. L Hutton 19 40,140 1948 4,167 10 ... =423. G Boycott 25 48,426 1970 3,109 9 ... =514. DCS Compton 22 38,942 1947 4,962 8 ... =514. RN Harvey 18 21,699 1953 3,506 8 ... =514. MEK Hussey 16 19,242 2001 2,711 8 ... =597. WG Grace 44 54,211 1871 2,739 7 ... =597. VT Trumper 19 16,939 1902 3,220 7 ... =597. BC Lara 20 22,156 1994 3,828 7 ... =687. GA Hick 26 41,112 1988 3,540 6 ... =746. IVA Richards 22 36,212 1976 3,080 5 ... =746. SR Waugh 21 24,052 1988 2,071 5 ... =795. DG Bradman 20 28,067 1930 4,368 4 ... =820. EW Dillon 15 11,006 1902 1,655 3 =820. R Kilner 13 14,707 1913 1,586 3 =820. TC Dodds 17 19,407 1947 2,147 3 =820. WGA Parkhouse 17 23,508 1950 2,284 3 =820. FA Lowson 10 15,321 1951 2,373 3 =820. RG Broadbent 14 12,800 1952 1,556 3 =820. AA Baig 20 12,367 1959 1,890 3 =820. JM Parker 14 11,254 1973 1,847 3 =820. DW Hookes 17 12,671 1977 1,634 3 =820. BA Edgar 15 11,304 1978 1,392 3 =820. RJ Blakey 19 14,674 1987 1,456 3 =820. UC Hathurusingha 16 10,862 1991 1,325 3 =820. ML Hayden 19 24,603 1993 2,760 3 =820. DR Martyn 16 14,630 1993 1,617 3 =834. GHG Doggart 14 10,054 1949 2,063 2 =834. AJ Moles 12 15,305 1987 2,238 2 =834. DP Ostler 14 10,856 1991 1,284 2 =834. AD Brown 18 15,806 1993 1,382 2 =834. A Symonds 16 14,477 1995 1,724 2 figures correct at end of English FC season 2009; full list available here
Trescothick is, indeed, one of the higher entries, in equal thirty-first place out of 838, amongst those who waited until their 17th year to post their highest aggregate. There are some good players who took even longer, though, including Bobby Abel, Frank Woolley, Arthur Milton, Graham Gooch, and Alec Stewart. Another of Somerset's star openers, Jimmy Cook, is in the upper reaches the list, due to the obvious circumstances of his career.
At the very top of the list is one of Kent's greatest runscorers (and one of Tottenham Hotspur's shortest-lived managers), Wally Hardinge. He first appeared for Kent in 1902 and, from 1911 to 1931, never failed to pass 1,000 runs per summer for them. However, it wasn't until 1928 – the 23rd of his 28 years playing FC cricket – that he reached his zenith, with 2,446 runs at 59.65, including the highest score of his FC career, 263* v. a pretty strong Gloucestershire attack.
It seems that good batsmen very seldom give up when their runscoring powers are in the ascendancy. Amongst the 10,000 club, there's only one player who stopped playing immediately after his highest-scoring year, and that's Derbyshire stalwart Alan Hill. Like Hardinge, his best season also included his highest FC innings, 172* v. Yorkshire at Sheffield.
At the bottom of the list, it turns out that no one who has gone on to rack up 10,000 FC runs has failed to surpass his debut year, but there are a few who never got past their sophomore effort. For some reason, this group appears to have a strong association with Birmingham.
Getting better all the time?
So much for viewing Trescothick's 2009 as a one-off burst of brilliance; what about the alternative view that it was merely the latest manifestation of an inexorable rise? Looking back at figure 2, it appears to be the case that his runscoring capacity has increased over the course of his career. But can we do something a bit more informative than eyeballing an apparent trend?
To anyone with a bit of stats about them, the answer is pretty obvious. We have two variables – years and year-by-year aggregates – and we want to know the extent to which one predicts the other: how much is the passage of time reflected in a batsman's year-end aggregates? The most common way of estimating this is to calculate a value that is sometimes called the coefficient of determination, but is more commonly known as r2. This figure estimates the amount of variation in one variable that is explained by the other; the higher the r2, the closer the correlation. If a batsman's totals went up (or down) by exactly the same amount every year, then his r2 would be 1: 100% of the variance in the observed aggregates is explained by the year-on-year trend. If, on the other hand, there were absolutely no evidence of a (linear) relationship between calendar year aggregates and time, then r2 would be 0.
The next table shows this value for the set of batsmen with 10,000 FC runs, including all those with an r2 of 0.5 or higher (indicating a reasonably clear correlation between time and runs). Note that, at this stage, we do not care whether the association is a positive or a negative one; for now, we are only seeking to identify the batsmen with the most consistent trends to their careers, regardless of whether they were getting better or worse.
Table 4: Batsmen with consistent trends in calendar-year aggregates, sorted by r2
Name CareerYrs Debut M I R Ave r2 1. WW Whysall 16 1910 371 601 21,592 38.76 0.939 2. A Flower 20 1986 223 372 16,379 54.06 0.797 3. JA Rudolph 13 1997 160 272 11,371 44.77 0.789 4. CJL Rogers 12 1998 149 263 12,865 52.30 0.781 5. M van Jaarsveld 16 1994 222 373 15,587 45.98 0.765 6. W Bates 11 1877 299 495 10,249 21.58 0.764 7. FA Lowson 10 1949 277 449 15,321 37.19 0.755 8. AG Prince 15 1995 166 265 10,204 44.75 0.739 9. EJ Smith 22 1904 496 814 16,997 22.39 0.712 10. G Dews 16 1946 376 642 16,803 28.53 0.704 11. TT Samaraweera 15 1995 207 285 11,233 48.00 0.674 12. JF Parker 15 1932 340 523 14,272 31.58 0.654 13. WE Bates 18 1907 406 684 15,964 24.41 0.652 14. WN Slack 12 1977 237 398 13,950 38.97 0.637 15. HFT Buse 17 1929 304 523 10,623 22.70 0.634 16. GE Tribe 14 1945 308 454 10,177 27.36 0.629 17. CS Elliott 14 1932 275 468 11,965 27.26 0.616 18. JC Balderstone 24 1961 390 619 19,034 34.11 0.605 19. AC Smith 18 1958 428 612 11,027 20.92 0.602 20. CC Inman 15 1956 255 422 13,113 34.51 0.595 21. C Charlesworth 20 1898 372 632 14,289 23.62 0.571 22. KS Duleepsinhji 9 1924 205 333 15,485 49.95 0.552 23. ME Trescothick 17 1993 254 438 16,645 40.11 0.549 24. TH Clark 13 1947 263 426 11,490 29.39 0.544 25. AJ Strauss 12 1998 181 321 13,090 42.92 0.543 26. MJ Di Venuto 18 1992 298 528 22,751 46.43 0.539 27. A Young 15 1911 311 539 13,159 25.45 0.539 28. H Morris 17 1981 314 544 19,785 40.30 0.532 29. JA Jameson 17 1960 361 611 18,941 33.35 0.528 30. MS Nichols 16 1924 483 756 17,823 26.56 0.525 31. GHG Doggart 14 1948 210 347 10,054 31.52 0.521 32. JL Hopwood 15 1923 400 575 15,548 29.90 0.512 33. HE Dollery 17 1933 436 717 24,414 37.50 0.508 34. N Pothas 17 1993 201 310 10,604 42.25 0.501 ... 96. KP Pietersen 12 1998 140 233 11,026 50.81 0.322 ... 169. GS Sobers 22 1953 383 609 28,314 54.87 0.225 ... 204. SJ Cook 24 1972 270 475 21,143 50.46 0.183 ... 253. DCS Compton 22 1936 515 839 38,942 51.85 0.146 ... 283. GA Hick 26 1983 526 871 41,112 52.24 0.126 ... 302. FE Woolley 29 1906 978 1,530 58,959 40.77 0.115 ... 307. WH Ponsford 14 1921 162 235 13,819 65.18 0.114 ... 361. SM Gavaskar 22 1966 348 563 25,834 51.36 0.087 ... 389. IVA Richards 22 1972 507 796 36,212 49.40 0.075 ... 395. MEK Hussey 16 1994 225 401 19,242 53.30 0.073 ... 451. WG Grace 44 1865 868 1,478 54,211 39.45 0.056 ... 495. GA Gooch 26 1973 580 990 44,846 48.85 0.043 ... 510. JB Hobbs 26 1905 832 1,325 61,760 50.66 0.038 ... 521. DG Bradman 20 1927 232 338 28,067 95.14 0.036 ... 528. IT Botham 20 1974 401 617 19,399 33.97 0.035 ... 571. H Sutcliffe 22 1919 754 1,098 50,670 52.02 0.026 ... 594. AR Morris 14 1940 162 250 12,614 53.68 0.022 ... 630. DJ Hussey 7 2003 132 203 10,048 55.21 0.015 ... 669. L Hutton 19 1934 513 814 40,140 55.29 0.009 ... 674. G Boycott 25 1962 609 1,014 48,426 56.77 0.009 ... 679. KS Ranjitsinhji 15 1893 307 500 24,692 56.37 0.008 ... 736. CK Nayudu 41 1916 207 344 11,825 35.94 0.004 ... 759. BC Lara 20 1988 261 440 22,156 51.89 0.002 ... 778. VT Trumper 19 1895 255 401 16,939 44.58 0.001 ... 791. WR Hammond 26 1920 634 1,005 50,551 56.04 0.001 ... 827. FMM Worrell 22 1942 207 326 15,025 54.24 0.000 figures correct at end of English FC season 2009; full list available here
As predicted, Trescothick is amongst those with the most obvious trends to their careers: an r2 of 0.549 is suggestive of a fairly clear correlation between time and runs, with over half of the variance in Trescothick's year-end aggregates explained by his year-on-year improvement.
The player at the top of this list is Nottinghamshire's leading runscorer of the 1920s, William "Dodger" Whysall. Whysall's Wisden obituary notes that he "matured slowly as a cricketer", which rather underplays the way in which he very gradually but very assuredly developed from a fairly ordinary performer into his county's most reliable batsman. Below, his year-by-year aggregates are plotted, with a regression line indicating the trend (ordinary least squares linear regression).
Figure 3: WW Whysall – first-class runs per calendar year, with fitted regression line

If you're wondering why his career came to an end despite showing such an encouraging trend, the sad answer is that Whysall died in late 1930. Alongside his status as the most consistently improving batsman in the record-books, he is probably also the only player to die of complications of an injury sustained on the dancefloor.
The figure below shows scatterplots for the batsmen at nos. 2–5 on the list. It is no surprise to see several current players, here: obviously, to begin a career with a positive trend is a more easily achievable feat than it is to sustain a year-on-year improvement from the beginning to the end of one's time in the game.
Figure 4: First-class runs per calendar year, with fitted regression lines, for selected batsmen

Because all the plots have been standardised to the same scale, the extent of year-on-year improvement can be seen in the gradient of the regression lines (the steeper the line, the more dramatic the improvement). So, of the four players whose career trends are pictured, Chris Rogers's career to date has shown the most meteoric rise, whereas Andy Flower's improvement was more gradual and sustained. This immediately suggests another question: whose career has shown the greatest year-on-year increase (i.e. who has the steepest regression line)? Before asking this, it is necessary to limit the dataset to those players for whom we can be reasonably confident that there is some sort of trend there at all. A straightforward way to do this is to exclude all the observations for which the regression model did not estimate a significant gradient (conventionally, statisticians tend to set the threshold for significance at p≤0.05 – this is loosely equivalent to saying we'll accept 1 false-positive per 20 analyses we conduct, although the precise definition of a p-value is not quite as intuitive to non-statisticians). It turns out that 177 of our 838 batsmen meet this criterion.
Having assembled a set of players whose careers appear to follow some sort of trend, we can sort it according to our best estimate of the average number of runs by which each player's year-end aggregates went up (or down) each year (technically, this is the beta coefficient from the regression model). This value, marked YrOnYr in the table, provides the gradient of the slopes seen in the scatterplots. Note that negative values (indicating that the player's year-end aggregates showed a decreasing trend) are possible.
Table 5: Batsmen with the most consistently positive trends in calendar-year aggregates
Name CareerYrs Debut M I R Ave r2 YrOnYr (95%CI) p 1. KS Duleepsinhji 9 1924 205 333 15,485 49.95 0.552 280.5 (54.6, 506.4) 0.022 2. CJL Rogers 12 1998 149 263 12,865 52.30 0.781 231.9 (145.5, 318.3) <0.001 3. WW Whysall 16 1910 371 601 21,592 38.76 0.939 190.8 (163.0, 218.7) <0.001 4. CF Walters 13 1923 245 427 12,145 30.75 0.492 157.8 (51.4, 264.2) 0.008 5. WN Slack 12 1977 237 398 13,950 38.97 0.637 155.7 (72.9, 238.5) 0.002 6. JA Rudolph 13 1997 160 272 11,371 44.77 0.789 129.9 (85.3, 174.4) <0.001 7. CC Inman 15 1956 255 422 13,113 34.51 0.595 124.0 (62.6, 185.3) 0.001 8. W Bates 11 1877 299 495 10,249 21.58 0.764 116.0 (67.3, 164.7) <0.001 9. M van Jaarsveld 16 1994 222 373 15,587 45.98 0.765 112.4 (76.6, 148.1) <0.001 10. CS Elliott 14 1932 275 468 11,965 27.26 0.616 111.7 (56.2, 167.2) 0.001 11. TH Clark 13 1947 263 426 11,490 29.39 0.544 110.7 (43.4, 178.0) 0.004 12. LB Fishlock 16 1931 417 699 25,376 39.34 0.306 106.8 (14.5, 199.1) 0.026 13. JF Parker 15 1932 340 523 14,272 31.58 0.654 105.2 (59.3, 151.1) <0.001 14. CL Smith 14 1978 269 466 18,028 44.40 0.362 100.4 (16.6, 184.2) 0.023 15. CAG Russell 19 1908 436 717 27,354 41.57 0.366 100.0 (32.7, 167.3) 0.006 16. C Lee 13 1952 271 472 12,129 26.60 0.415 99.5 (21.1, 177.9) 0.017 17. H Morris 17 1981 314 544 19,785 40.30 0.532 98.9 (47.8, 149.9) 0.001 18. JA Jameson 17 1960 361 611 18,941 33.35 0.528 97.2 (46.6, 147.7) 0.001 19. MJ Di Venuto 18 1992 298 528 22,751 46.43 0.539 97.1 (49.5, 144.8) 0.001 20. G Dews 16 1946 376 642 16,803 28.53 0.704 95.9 (60.2, 131.6) <0.001 ... 26. A Flower 20 1986 223 372 16,379 54.06 0.797 88.9 (66.6, 111.2) <0.001 ... 57. ME Trescothick 17 1993 254 438 16,645 40.11 0.549 65.6 (32.9, 98.4) 0.001 ... 74. GS Sobers 22 1953 383 609 28,314 54.87 0.225 58.8 (7.9, 109.6) 0.026 ... 85. SJ Cook 24 1972 270 475 21,143 50.46 0.183 55.2 (3.6, 106.8) 0.037 ... 149. AP Lucas 29 1874 256 435 10,263 26.38 0.187 -13.6 (-24.8, -2.4) 0.019 150. KJ Key 26 1882 367 567 13,008 26.23 0.158 -21.2 (-41.9, -0.6) 0.044 151. FH Gillingham 22 1903 210 352 10,050 30.64 0.353 -25.6 (-41.8, -9.5) 0.004 152. FR Brown 25 1930 355 536 13,325 27.36 0.174 -25.7 (-49.8, -1.5) 0.038 153. PA Perrin 29 1896 537 918 29,709 35.92 0.297 -26.0 (-41.9, -10.2) 0.002 154. DB Close 35 1949 785 1,225 34,994 33.23 0.188 -26.2 (-45.6, -6.9) 0.009 155. Hanif Mohammad 25 1951 238 370 17,059 52.33 0.178 -29.0 (-55.9, -2.1) 0.036 156. KWR Fletcher 27 1962 730 1,167 37,665 37.78 0.192 -30.1 (-55.6, -4.7) 0.022 157. CP McGahey 24 1894 437 751 20,723 30.21 0.178 -30.8 (-60.2, -1.5) 0.040 158. AF Wensley 20 1922 399 595 10,875 20.48 0.212 -33.0 (-64.5, -1.5) 0.041 159. NH Fairbrother 20 1983 366 580 20,612 41.22 0.327 -33.7 (-57.6, -9.7) 0.008 160. JF Steele 17 1970 379 605 15,054 28.95 0.241 -41.2 (-81.5, -0.9) 0.046 161. AA Baig 20 1955 235 391 12,367 34.07 0.235 -42.7 (-80.9, -4.5) 0.030 162. LH Tennyson 22 1913 477 759 16,828 23.34 0.397 -44.6 (-70.2, -19.0) 0.002 163. JP Stephenson 21 1985 303 512 14,773 32.40 0.258 -45.5 (-82.6, -8.4) 0.019 164. APF Chapman 20 1920 392 554 16,309 31.98 0.380 -48.5 (-79.1, -17.8) 0.004 165. AC Smith 18 1958 428 612 11,027 20.92 0.602 -50.0 (-71.5, -28.4) <0.001 166. FA Tarrant 24 1899 329 541 17,952 36.41 0.203 -50.6 (-95.0, -6.3) 0.027 167. KJ Hughes 17 1975 216 368 12,711 36.53 0.236 -52.3 (-104.1, -0.5) 0.048 168. PJ Watts 18 1959 375 607 14,449 27.95 0.356 -53.7 (-91.9, -15.4) 0.009 169. TG Evans 21 1939 465 753 14,882 21.23 0.388 -55.4 (-88.8, -22.0) 0.003 170. JR Mason 22 1893 339 557 17,337 33.28 0.427 -57.7 (-88.9, -26.6) 0.001 171. ERT Holmes 22 1924 301 465 13,598 32.85 0.287 -57.8 (-100.2, -15.3) 0.010 172. RR Relf 18 1905 302 529 14,522 28.42 0.304 -65.3 (-117.7, -12.9) 0.018 173. RES Wyatt 30 1923 737 1,141 39,405 40.05 0.378 -73.2 (-109.5, -36.8) <0.001 174. LJ Lenham 14 1956 300 539 12,796 26.17 0.433 -83.2 (-143.0, -23.3) 0.010 175. AJ Moles 12 1986 230 416 15,305 40.70 0.474 -89.7 (-156.2, -23.1) 0.013 176. GHG Doggart 14 1948 210 347 10,054 31.52 0.521 -101.7 (-163.0, -40.4) 0.004 177. FA Lowson 10 1949 277 449 15,321 37.19 0.755 -177.4 (-259.8, -95.0) 0.001 figures correct at end of English FC season 2009; full list available here
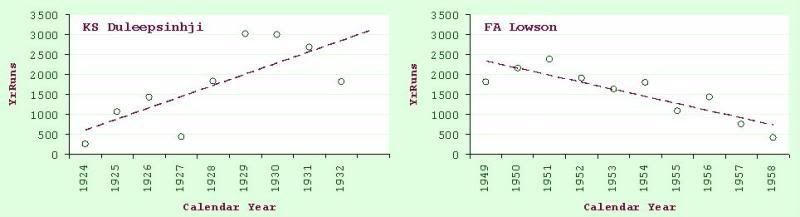
Several of the names at the head of this list are familiar from our previous analysis, but our leader is someone to whom we have not paid particular attention, as yet. Kumar Shri Duleepsinhji's career only spanned nine seasons, but that was long enough for him to rack up over 15,000 FC runs (including 50 centuries) at an average a hair under 50. Like his uncle, Ranji, he was also extremely successful in his few test matches in England colours. One reason why his career shows such a dramatic upward trend is that he was cut off just as he was reaching his peak. The innings that turned out to be his last in FC cricket was the 90 he made - we can assume, with his renowned elegance - at Taunton in 1932. Afterwards, he collapsed, and was forced to withdraw from England's forthcoming tour to Australia (which would, of course, be remembered for other reasons entirely). Ultimately, he was compelled to give the game up completely, on his doctors' orders. He was only 27 at the time.
At the other end of the spectrum, we find Frank Lowson, best known as Len Hutton's opening partner at Yorkshire in the last part of the great man's career. Lowson was in his thirties by the time he made his FC debut in 1949. His first three seasons were all extremely successful, culminating in selection for England in 1951, followed by a tour to the subcontinent that winter. Unhappily, he did not distinguish himself in his test outings, and his career began a slide that was never arrested until he bowed out, aged 43, in 1958. To be sure, amassing 10,000 FC runs is an achievement of which any batsman can be proud; nevertheless, amongst those to achieve this landmark, none had so steep a decline as Lowson, who scored an average of 177 fewer runs each year of his career.
Figure 5: First-class runs per calendar year, with fitted regression lines, for KS Duleepsinhji and FA Lowson
The apparent declines of two notable England captains – Brian Close and Bob Wyatt – need to be taken with a pinch of a salt. For almost a decade after his competitive career came to an end, Close had one FC outing per year, leading his own XI at the Scarborough festival. Similarly, Wyatt's career had a six-year coda, featuring very sporadic appearances for the MCC and – at a time when some of their fixtures attracted FC status – the Free Foresters. For each player, if analysis is confined to the competitive portion of their careers, the regression model no longer identifies a significant negative trend.
To conclude, we should return to the player who sparked off this line of enquiry in the first place. According to this analysis, Marcus Trescothick is what an American sportscaster might call the 57th improvingest batsman in FC history. He has tended to total 65.6 additional runs per year he has been in the game, which means that, if the linear trend is continued, we would expect him to amass 1,569 FC runs in 2010. Of course, Somerset's fans would be delighted if this trend – or something like it – extends for many more years to come.
Figure 6: ME Trescothick – first-class runs per calendar year, with fitted regression line




No comments:
Post a Comment